What Is The Average Rate Of Change From X = 0 To X = 5?

$y$	2005	2006	2007	2008	2009	2010	2011	2012
$C\left(y\correct)$	2.31	2.62	2.84	3.xxx	2.41	two.84	3.58	iii.68

The toll change per year is a rate of change considering it describes how an output quantity changes relative to the change in the input quantity. Nosotros can see that the price of gasoline in the table higher up did not change by the aforementioned amount each yr, and so the rate of change was not constant. If we use merely the beginning and ending data, we would be finding the average charge per unit of change over the specified period of fourth dimension. To find the average rate of modify, we divide the alter in the output value by the change in the input value.

Boilerplate rate of change=

$\frac{\text{Alter in output}}{\text{Modify in input}}$

$\frac{\Delta y}{\Delta 10}$

$\frac{{y}_{two}-{y}_{one}}{{x}_{2}-{x}_{1}}$

$\frac{f\left({x}_{ii}\correct)-f\left({10}_{1}\right)}{{x}_{2}-{x}_{1}}$

The Greek letter of the alphabet

$\Delta$

(delta) signifies the modify in a quantity; we read the ratio every bit "delta-y over delta-10" or "the change in

$y$

divided by the change in

$x$

." Occasionally we write

$\Delta f$

instead of

$\Delta y$

, which withal represents the alter in the office'due south output value resulting from a change to its input value. It does not mean we are changing the function into some other function.

In our example, the gasoline toll increased past $1.37 from 2005 to 2012. Over 7 years, the average rate of change was

$\frac{\Delta y}{\Delta x}=\frac{{i.37}}{\text{vii years}}\approx 0.196\text{ dollars per year}$

On boilerplate, the price of gas increased by about 19.6¢ each year.

Other examples of rates of change include:

A population of rats increasing by twoscore rats per calendar week
A car traveling 68 miles per hour (distance traveled changes past 68 miles each hour every bit time passes)
A car driving 27 miles per gallon (distance traveled changes by 27 miles for each gallon)
The electric current through an electric circuit increasing by 0.125 amperes for every volt of increased voltage
The amount of money in a college account decreasing past $4,000 per quarter

A Full general Notation: Rate of Change

A charge per unit of change describes how an output quantity changes relative to the change in the input quantity. The units on a charge per unit of alter are "output units per input units."

The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.

$\frac{\Delta y}{\Delta 10}=\frac{f\left({x}_{2}\correct)-f\left({x}_{1}\correct)}{{x}_{two}-{ten}_{1}}$

How To: Given the value of a office at different points, calculate the average rate of change of a function for the interval betwixt 2 values
${x}_{ane}$
and
${10}_{two}$
.

Calculate the deviation
${y}_{2}-{y}_{1}=\Delta y$
.
Calculate the difference
${x}_{ii}-{ten}_{one}=\Delta ten$
.
Find the ratio
$\frac{\Delta y}{\Delta 10}$
.

Example 1: Computing an Average Rate of Modify

Using the information in the table below, find the average rate of change of the cost of gasoline betwixt 2007 and 2009.

$y$	2005	2006	2007	2008	2009	2010	2011	2012
$C\left(y\right)$	2.31	2.62	2.84	3.30	2.41	2.84	3.58	3.68

Solution

In 2007, the price of gasoline was $ii.84. In 2009, the cost was $2.41. The average rate of change is

$\brainstorm{cases}\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{10}_{1}}\\ {}\\=\frac{2.41-2.84}{2009 - 2007}\\ {}\\=\frac{-0.43}{2\text{ years}}\\{} \\={-0.22}\text{ per year}\end{cases}$

Analysis of the Solution

Notation that a decrease is expressed by a negative change or "negative increase." A rate of change is negative when the output decreases equally the input increases or when the output increases every bit the input decreases.

The post-obit video provides some other example of how to observe the boilerplate charge per unit of change between two points from a tabular array of values.

Endeavour It 1

Using the data in the table beneath, notice the average rate of change betwixt 2005 and 2010.

$y$	2005	2006	2007	2008	2009	2010	2011	2012
$C\left(y\right)$	2.31	two.62	2.84	3.30	2.41	ii.84	3.58	iii.68

Solution

Instance ii: Computing Average Charge per unit of Change from a Graph

Given the function

$m\left(t\right)$

shown in Figure ane, find the average rate of change on the interval

$\left[-1,2\right]$

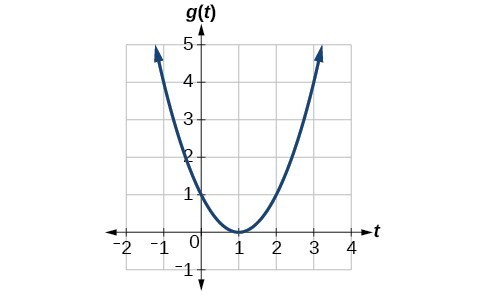Graph of a parabola. Effigy ane

Solution

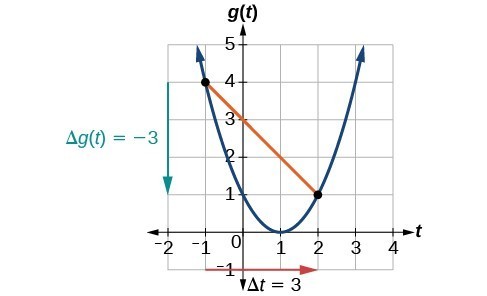Graph of a parabola with a line from points (-1, 4) and (2, 1) to show the changes for g(t) and t. Figure 2

$t=-ane$

, the graph shows

$chiliad\left(-1\right)=4$

. At

$t=2$

, the graph shows

$g\left(ii\correct)=1$

The horizontal change

$\Delta t=3$

is shown by the carmine arrow, and the vertical change

$\Delta chiliad\left(t\right)=-iii$

is shown by the turquoise pointer. The output changes by –3 while the input changes by 3, giving an average rate of change of

$\frac{1 - 4}{2-\left(-ane\right)}=\frac{-3}{three}=-1$

Assay of the Solution

Note that the order we choose is very important. If, for example, we use

$\frac{{y}_{2}-{y}_{1}}{{ten}_{1}-{x}_{2}}$

, we will not get the right respond. Decide which point will be 1 and which point will be 2, and keep the coordinates stock-still as

$\left({ten}_{i},{y}_{1}\right)$

and

$\left({x}_{two},{y}_{2}\right)$

Case 3: Calculating Average Rate of Change from a Table

Afterwards picking up a friend who lives 10 miles away, Anna records her altitude from abode over time. The values are shown in the tabular array below. Find her average speed over the first vi hours.

t (hours)	0	ane	ii	3	four	5	half dozen	seven
D(t) (miles)	10	55	90	153	214	240	282	300

Solution

Here, the average speed is the average rate of alter. She traveled 282 miles in half dozen hours, for an average speed of

$\begin{cases}\\ \frac{292 - 10}{half dozen - 0}\\ {}\\ =\frac{282}{6}\\{}\\ =47 \end{cases}$

The boilerplate speed is 47 miles per 60 minutes.

Analysis of the Solution

Because the speed is non abiding, the boilerplate speed depends on the interval chosen. For the interval [two,3], the average speed is 63 miles per hour.

Example iv: Computing Average Rate of Change for a Function Expressed as a Formula

Compute the boilerplate rate of change of

$f\left(x\correct)={x}^{2}-\frac{one}{x}$

on the interval

$\text{[two,}\text{iv].}$

Solution

We can start by computing the function values at each endpoint of the interval.

$\brainstorm{cases}f\left(two\right)={2}^{two}-\frac{1}{ii}& f\left(4\right)={4}^{two}-\frac{ane}{4} \\ =iv-\frac{1}{2} & =16-{1}{iv} \\ =\frac{7}{2} & =\frac{63}{4} \end{cases}$

Now we compute the average charge per unit of change.

$\brainstorm{cases}\text{Average rate of change}=\frac{f\left(4\right)-f\left(2\correct)}{4 - 2} \\{}\\\text{ }=\frac{\frac{63}{4}-\frac{seven}{2}}{iv - two} \\{}\\ \text{ }\text{ }=\frac{\frac{49}{4}}{2} \\ {}\\ \text{ }=\frac{49}{viii} \end{cases}$

The following video provides another example of finding the average rate of change of a function given a formula and an interval.

Try Information technology 2

Find the boilerplate rate of change of

$f\left(x\right)=x - 2\sqrt{x}$

on the interval

$\left[1,9\right]$

Solution

Example 5: Finding the Average Rate of Change of a Force

The electrostatic forcefulness

$F$

, measured in newtons, betwixt two charged particles can be related to the altitude between the particles

$d$

, in centimeters, past the formula

$F\left(d\right)=\frac{2}{{d}^{2}}$

. Find the average rate of change of force if the altitude between the particles is increased from 2 cm to 6 cm.

Solution

We are computing the average charge per unit of change of

$F\left(d\right)=\frac{two}{{d}^{2}}$

on the interval

$\left[2,6\right]$

$\begin{cases}\text{Average rate of change }=\frac{F\left(six\right)-F\left(2\correct)}{6 - ii}\\ {}\\ =\frac{\frac{2}{{six}^{2}}-\frac{ii}{{two}^{two}}}{6 - two} & \text{Simplify}. \\ {}\\=\frac{\frac{2}{36}-\frac{two}{4}}{iv}\\{}\\ =\frac{-\frac{16}{36}}{4}\text{Combine numerator terms}.\\ {}\\=-\frac{1}{9}\text{Simplify}\finish{cases}$

The average charge per unit of change is

$-\frac{1}{nine}$

newton per centimeter.

Example vi: Finding an Average Rate of Modify as an Expression

Find the average rate of change of

$yard\left(t\correct)={t}^{2}+3t+1$

on the interval

$\left[0,a\correct]$

. The reply will be an expression involving

$a$

Solution

Nosotros apply the average charge per unit of change formula.

$\text{Average charge per unit of change}=\frac{one thousand\left(a\right)-yard\left(0\right)}{a - 0}\text{Evaluate}$

$\frac{\left({a}^{ii}+3a+1\right)-\left({0}^{two}+three\left(0\correct)+one\right)}{a - 0}\text{Simplify}.$

$\frac{{a}^{ii}+3a+1 - one}{a}\text{Simplify and gene}.$

$\frac{a\left(a+3\right)}{a}\text{Divide by the common gene }a.$

This consequence tells the states the average rate of modify in terms of

$a$

between

$t=0$

and any other betoken

$t=a$

. For example, on the interval

$\left[0,5\correct]$

, the average rate of alter would be

$v+3=viii$

Try It 3

Observe the boilerplate rate of change of

$f\left(10\right)={10}^{2}+2x - 8$

on the interval

$\left[5,a\right]$

Solution

Licenses and Attributions

Source: https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/find-the-average-rate-of-change-of-a-function/

Posted by: chavezhond1975.blogspot.com